선형회귀란 ?
선형 회귀(Linear Regression)는 회귀 문제를 예측할 때 사용하는 알고리즘 중 하나이다.
'독립 변수가 커질 때 종속 변수가 크거나 작게 변하는' 관계를 모델링 하는 것이다. 선형회귀는 보통 하나 이상의 독립 변수를 사용하여 모델링한다. 이 때, 독립 변수가 둘 이상이면 '다중선형회귀( multiple linear regression)'라고 한다.
다중선형회귀란?
행렬식으로 나타내보면 다음과 같다.

tensorflow를 이용할 때 placeholder 생성 시 shape을 잘 맞춰주어야 한다. 그래야 matmul 함수를 사용했을 때 식이 성립되기 때문이다. 예를 들어 위의 식은 [ 3, 1 ] * [ 1 * 3 ] = [ 1 * 1 ] 이므로 성립 가능하다. 이 과정을 수식으로 나타내 가설을 세우면 다음과 같다.
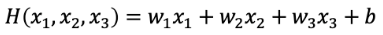

단순선형회귀에서 사용하던 가설에 x값을 여러개 추가하여 위의 식으로 가설을 세운다. 독립변수가 추가되어 변경된 가설을 사용하면 cost function식 또한 아래와 같이 변경된다.
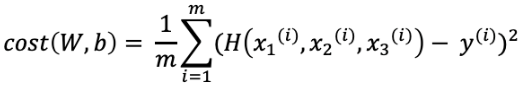
code
1 ) sklearn module로 Solar.R, Wind, Temp가 170, 7.4, 67일 때의 Ozone 수치를 예측해보자.
# module import
from sklearn import linear_model
import numpy as np
import pandas as pd
# data load
df = pd.read_csv('/machine-deep-learning/machine learning/data/ozone.csv')
df = df[['Ozone','Solar.R','Wind','Temp']]
결측치를 확인해보자
df.isnull().sum()Ozone 37
Solar.R 7
Wind 0
Temp 0
dtype: int64
결측치를 제거해주자
df = df.dropna(how='any', inplace=False)
이상치를 확인해보자
# 다음의 코드를 하나씩 실행한다
plt.boxplot(df["Solar.R"])
plt.boxplot(df["Temp"])
plt.boxplot(df["Ozone"])
plt.boxplot(df["Wind"])
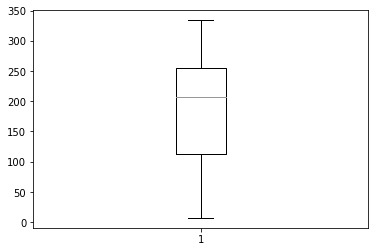


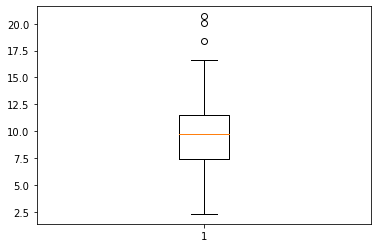
Ozone과 Wind에 이상치가 있으므로 제거해주자
## ozone
q1, q3 = np.percentile(df['Ozone'],[25,75])
irq = q3 - q1
upper = q3 + irq * 1.5
mask = df['Ozone'] > upper
df = df.loc[~mask]
## wind
q_1, q_3 = np.percentile(df['Wind'],[25,75])
irq = q_3 - q_1
up = q_3 + irq * 1.5
mask2 = df['Wind'] > up
df = df.loc[~mask2]
학습시킨 뒤 예측하면?
# learning data
X = df[['Solar.R','Wind','Temp']]
Y = df['Ozone']
# learning
lm = linear_model.LinearRegression()
lm.fit(X,Y)
# prediction
prediction = lm.predict([[170, 7.4, 67]])
print('예측값은 : {}'.format(prediction))[27.97594664]
2 ) tensorflow로 점수가 80, 90, 50일 때의 출력값을 예측해보자.
import tensorflow as tf
import numpy as np
import pandas as pd
# 사용할 데이터
x_data = [[73,80,75],
[93,88,93],
[89,91,90],
[96,98,100],
[73,66,70]]
y_data = [[152],[185],[180],[196],[142]]# plceholder
# 행이 몇개 입력될지 모르기 때문에 None으로 설정
# 열은 3개로 고정이기 때문에 X의 열은 3
# 학습시키는 종속 변수의 열은 1개이므로 Y의 열은 1
X = tf.placeholder(shape = [None,3], dtype = tf.float32)
Y = tf.placeholder(shape = [None,1], dtype = tf.float32)
# weight, bias
# x가 3열이기 때문에 [3,1]
W = tf.Variable(tf.random_normal([3,1]),name="Weight")
b = tf.Variable(tf.random_normal([1]), name="bias")
# Hypothesis
# matmul : 행렬계산
H = tf.matmul(X,W) + b
# cost function
cost = tf.reduce_mean(tf.square(H-Y))
# train node 생성
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.00000001)
train = optimizer.minimize(cost)
# runner session 필요
sess = tf.Session()
sess.run(tf.global_variables_initializer()) # 그래프 초기화
# learning
for step in range(30000):
_,cost_val = sess.run([train,cost],
feed_dict={
X : x_data,
Y : y_data
})
if step % 3000 == 0:
print("cost값은 : {}".format(cost_val))
# prediction
print(sess.run(H, feed_dict = {X : [[80,90,50], ] }))# 학습 중 cost값의 변화
cost값은 : 1362.474853515625
cost값은 : 113.27144622802734
cost값은 : 24.22825050354004
cost값은 : 17.8582763671875
cost값은 : 17.380420684814453
cost값은 : 17.322494506835938
cost값은 : 17.292247772216797
cost값은 : 17.266658782958984
cost값은 : 17.241649627685547
cost값은 : 17.216651916503906
# 결과는
[[113.24003]]
다중선형회귀(Multiple Linear Regression) - 파이썬 코드 예제 - 아무튼 워라밸
파이썬 scikit-learn으로 다중선형회귀(Multiple Linear Regression) 분석하는 방법을 코드 예제와 함께 살펴보자.
hleecaster.com
[Python] 다중 회귀 분석(Multiple Regression)
안녕하세요 불탄오징어입니다. Python 공부도 할 겸 틈틈히 통계 분석 모형들을 하나씩 수행해보려고 합니다. Python이 대세라서 한다기보다는 순수한 재미로 해볼려고 합니다. 현재는 업무에 Python
bongury.tistory.com
[TensorFlow] 다중 선형 회귀분석 multi-value linear regression :: 마이자몽
출처 : https://www.tensorflow.org 다중 선형 회귀(Multi-Value Linear Regression) 단순 선형 회귀분석에서는 하나의 독립변수 x값에 대해 하나의 종속변수 y값을 찾는 작업을 했었다. 하지만, 실제로 사용하는..
myjamong.tistory.com
'AI > Experiment' 카테고리의 다른 글
| 05. 릿지 회귀, 라쏘 회귀 ( Ridge, Lasso ) (0) | 2020.05.15 |
|---|---|
| 04. 다항 회귀( Polynomial Regression ) (0) | 2020.05.14 |
| 02. 단순선형회귀( Simple Linear Regression ) (0) | 2020.05.11 |
| 01. 머신러닝 모델 평가 방법 (0) | 2020.05.10 |
| 00. 머신러닝 개요 (0) | 2020.05.10 |