단순선형회귀와의 비교
가장 처음 공부한 선형회귀는 MSE를 최소화하는 기울기와 절편을 찾았다.
릿지와 라쏘는 오차값에 규제항 또는 벌점항을 추가하여 좀 더 단순화된 모델, 일반화된 모델을 제공한다.
이렇게 단순화하거나 일반화된 모델에서는 훈련셋에 덜 과적합 되기 때문에 테스트셋에 더 적합한 모델을 만들 수 있다.
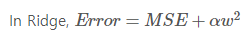

릿지는 w의 제곱항(L2 규제)을, 라쏘는 w의 절대값(L1 규제)를 추가한다. α는 규제의 강도를 의미한다.
아래의 코드로 MSE, L2, L1이 다른 부분을 살펴보자.
# module import
%pylab inline
import numpy as np
import matplotlib.pyplot as plt
# plot의 크기 설정
fig = plt.figure(figsize=[12,6])
# 범위 설정( -10 에서 10까지, 100개)
rng = np.linspace(-10,10,100)
# mse
mse = (0.5*(rng-3))**2 + 30
# l2는 제곱값
l2 = rng**2
# l1은 절대값
l1 = 5*np.abs(rng)
# ridge, lasso 계산
ridge = mse + l2
lasso = mse + l1
plt.subplot(1,2,1)
plt.plot(rng,mse,label='MSE')
plt.plot(rng,l2,'--',label='L2')
plt.plot(rng,ridge, lw=2, label='Ridge')
plt.xlabel('w'); plt.ylabel('Error')
plt.legend()
plt.subplot(1,2,2)
plt.plot(rng,mse,label='MSE')
plt.plot(rng,l1,'--',label='L1')
plt.plot(rng,lasso, lw=2, label='Lasso')
plt.xlabel('w'); plt.ylabel('Error')
plt.legend()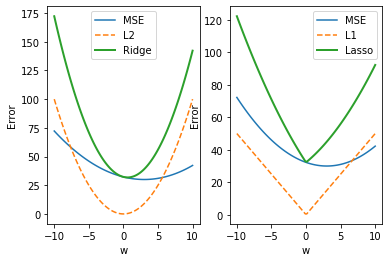
릿지와 라쏘회귀의 Error의 최소값 위치가 w값이 0쪽으로 치우쳐짐을 확인할 수 있다.
또한, 라쏘는 릿지보다 최소값 근처에서 기울기가 큼을 알 수 있다.
두 식 모두 경사하강법을 사용하기 때문에 릿지는 w가 천천히 0으로 향하지만 라쏘는 w가 빨리 0으로 향한다.
---
또한 규제의 강도를 의미하는 alpha값이 커질수록 w가 0으로 향하는 정도와 속도가 커진다.
예제로 살펴보자
보스턴 주택가격 데이터셋 활용
1. 단순 선형 회귀
# module import
import mglearn
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 학습
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)
lr = LinearRegression().fit(X_train, y_train)
# 결과 출력
print('훈련 세트 점수 : {:.2f}'.format(lr.score(X_train, y_train)))
print('테스트 세트 점수 : {:.2f}'.format(lr.score(X_test, y_test)))
훈련 세트 점수 : 0.95
테스트 세트 점수 : 0.61훈련, 테스트 세트 사이의 성능 차이는 모델이 과대적합되었다는 신호이므로 복잡도를 제어할 수 있는 모델을 사용해야 한다.
2. 리지 회귀
리지 회귀에서 가중치 선택은 1 ) 훈련 데이터를 잘 예측하기 위해 2 ) 추가 제약 조건을 만족시키기 위해 사용된다. 가중치의 절댓값을 가능한 작게 만들어 모든 특성이 출력에 주는 영향을 최소한으로 만든다.(기울기를 작게!) 이런 제약을 규제라고 하며, 과대적합이 되지 않도록 모델을 강제로 제한한다. 리지 회귀의 규제 방식을 L2 규제라고 한다.
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print('훈련 세트 점수 : {:.2f}'.format(ridge.score(X_train, y_train)))
print('테스트 세트 점수 : {:.2f}'.format(ridge.score(X_test, y_test)))
# alpha 값을 조절해보자
ridge_10 = Ridge(alpha=10).fit(X_train, y_train)
print('훈련 세트 점수 : {:.2f}'.format(ridge_10.score(X_train, y_train)))
print('테스트 세트 점수 : {:.2f}'.format(ridge_10.score(X_test, y_test)))
ridge_1 = Ridge(alpha=0.1).fit(X_train, y_train)
print('훈련 세트 점수 : {:.2f}'.format(ridge_1.score(X_train, y_train)))
print('테스트 세트 점수 : {:.2f}'.format(ridge_1.score(X_test, y_test)))
# alpha 값 default = 1
훈련 세트 점수 : 0.89
테스트 세트 점수 : 0.75
# alpha = 10
훈련 세트 점수 : 0.79
테스트 세트 점수 : 0.64
# alpha = 0.1
훈련 세트 점수 : 0.93
테스트 세트 점수 : 0.77alpha가 작을 때 테스트셋의 점수가 높아짐을 알 수 있다.
alpha 값을 높이면 계수를 0에 더 가깝게 만들기 때문에 훈련 세트의 성능이 나빠지지만 일반화에 도움을 준다.
alpha 값을 줄이면 계수에 대한 제약이 그만큼 풀리면서 계수를 거의 제한하지 않아 선형회귀모델과 비슷해진다.
alpha값을 고정하고 훈련 데이터의 크기를 변화시켰을 때 모델의 성능변화를 그려보자. (학습 곡선, learning curve)
mglearn.plots.plot_ridge_n_samples()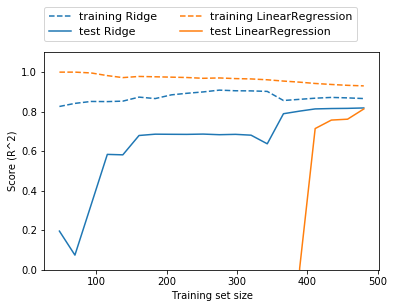
위의 그림을 통해 다음을 알 수 있다.
1 ) 리지와 선형 회귀 모두 훈련 세트의 점수가 테스트 세트의 점수보다 높다
2 ) 리지에는 규제가 적용되므로 리지의 훈련 데이터 점수가 전체적으로 선형회귀 훈련 데이터 점수보다 낮다
3 ) 테스트 데이터에서는 리지 회귀의 점수가 더 높다 ( 특히 작은 데이터셋 !!! )
4 ) 두 성능의 모델은 데이터가 많아질수록 좋아진다
5 ) 데이터를 충분히 준다면, 규제 항은 덜 중요해져서 리지와 선형회귀의 성능이 같아질 것이다
6 ) 데이터가 많아질수록 모델이 데이터를 기억하거나 과대적합하기 어려워 선형 회귀의 훈련 데이터 성능이 감소한다
3. 라쏘 회귀
라쏘 회귀 또한 리지 회귀에서와 같이 계수를 0에 가깝게 만들고자한다. 라쏘의 규제는 L1이라고 하며, 결과로 정말 어떤 계수는 0이 되기도 한다. 따라서 완전히 제외되는 특성이 생긴다. ( 특성 선택이 feature selection 자동으로 이뤄진다 ) 일부 계수를 0으로 만들면 모델을 이해하기 쉬워지고 이 모델의 가장 중요한 특성인지 알 수 있다.
from sklearn.linear_model import Lasso
# alpha = dafualt = 1
lasso = Lasso().fit(X_train, y_train)
print('훈련 세트 점수 : {:.2f}'.format(lasso.score(X_train, y_train)))
print('테스트 세트 점수 : {:.2f}'.format(lasso.score(X_test, y_test)))
print('기존 특성 개수 : ', len(X_train[0]))
print('사용한 특성의 개수 : ', np.sum(lasso.coef_ != 0))
훈련 세트 점수 : 0.29
테스트 세트 점수 : 0.21
기존 특성 개수 : 104
사용한 특성의 개수 : 4104개 중의 4개 특성많 사용하다보니 결과가 매우 좋지 않다. alpha값을 줄여보자.
lasso01 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print('훈련 세트 점수 : {:.2f}'.format(lasso01.score(X_train, y_train)))
print('테스트 세트 점수 : {:.2f}'.format(lasso01.score(X_test, y_test)))
print('기존 특성 개수 : ', len(X_train[0]))
print('사용한 특성의 개수 : ', np.sum(lasso01.coef_ != 0))
훈련 세트 점수 : 0.90
테스트 세트 점수 : 0.77
기존 특성 개수 : 104
사용한 특성의 개수 : 33alpha값을 줄일 때는 반복 실행하는 최대 횟수 값인 max_iter을 설정해주어야 한다. 결과를 살펴보니 훈련세트와 데이터세트에서의 성능이 좋아짐을 알 수 있다. 성능은 릿지 회귀보다 좋으면서 사용된 특성은 104개 중 33개이므로 모델 분석에 용이할 것이다.
하지만, alpha값을 너무 낮추면 규제 효과가 없어져 과대적합된다. 결국 선형회귀와 결과가 비슷해진다.
lasso0001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print('훈련 세트 점수 : {:.2f}'.format(lasso0001.score(X_train, y_train)))
print('테스트 세트 점수 : {:.2f}'.format(lasso0001.score(X_test, y_test)))
print('기존 특성 개수 : ', len(X_train[0]))
print('사용한 특성의 개수 : ', np.sum(lasso0001.coef_ != 0))
훈련 세트 점수 : 0.95
테스트 세트 점수 : 0.64
기존 특성 개수 : 104
사용한 특성의 개수 : 96
실제로 이 두 모델 중 보통 리지 회귀를 선호한다. 하지만 특성이 많고 그 중 일부분만 중요할 때는 라쏘 회귀를 선호하기도 한다. 분석하기 쉬운 모델을 원한다면 라쏘회귀가 입력 특성 중 일부만 사용하여 쉽게 해석할 수 있는 모델을 만들 수 있다.
이후, scikit-learn은 라쏘와 회귀의 penalty를 결합한 ElasticNet도 제공한다. 이는 L1, L2 규제를 위한 매개변수 두 개를 조정하면 최고의 성능을 낸다 !!
'AI > Experiment' 카테고리의 다른 글
| 07. 로지스틱 회귀( Logistic Regression ) (0) | 2020.05.18 |
|---|---|
| 06. 선형 회귀의 한계점 (0) | 2020.05.17 |
| 04. 다항 회귀( Polynomial Regression ) (0) | 2020.05.14 |
| 03. 다중선형회귀( Multiple Linear Regression ) (0) | 2020.05.13 |
| 02. 단순선형회귀( Simple Linear Regression ) (0) | 2020.05.11 |