분산분석이란?
기존에 공부했던 A/B 검정은 두 개의 그룹을 비교하였다. 그렇다면 A,B,C,D 그룹의 데이터를 비교한다고 가정하자. 여러 그룹 간의 통계적으로 유의미한 차이를 검정하는 통계적 절차를 분산분석(ANOVA ; analysis of variance)이라고 한다.
예를 살펴보자.
| Page 1 | Page 2 | Page 3 | Page 4 | |
| 164 | 178 | 175 | 155 | |
| 172 | 191 | 193 | 166 | |
| 177 | 182 | 171 | 164 | |
| 156 | 185 | 163 | 170 | |
| 195 | 177 | 176 | 168 | |
| 평균 | 172 | 185 | 176 | 162 |
이런 데이터가 있다면, A/B 검정을 할 때는 (1,2) (1,3) (1,4) (2,3) (2,4) (3,4) 의 모든 페이지를 비교해야 한다.
하지만 이렇게 한 쌍씩 비교하는 횟수가 증가할수록 우연히 일어난 일에 속을 가능성이 커진다.
따라서 모든 페이지가 동일한 기본적인 점착성을 갖는지? 이들 사이의 차이는 우연에 의한 것인지? 원래 4페이지에 할당된 세션 시간 또한 무작위로 할당되었는지? 등의 질문을 다루는 전체적인 총괄검정을 할 수 있다. ANOVA는 이 검정에 사용된다.
분산분석의 조건
1. 정규성 : 각각의 그룹에서 변인은 정규분포이다
2. 분산의 동질성 : y의 모집단 분산은 각각의 모집단에서 동일하다
3. 관찰의 독립성 : 각각의 모집단에서 크기가 각각인 표본들이 독립적으로 표집되어있다.
분산(variance)의 중요성
평균 값은 동일하지만 분산 값이 다름으로 인해 전체의 데이터 양상이 달라짐을 살펴볼 수 있다.
# module 설치
import scipy.stats as stats
import pandas as pd
import urllib
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# 표준편차를 0.1로 설정
centers = [5,5.3,4.5]
std = 0.1
colors = 'brg'
data_1 = []
for i in range(3):
# stats.norm으로 평균, 표준편차를 만족하는 점 100개 생성
data_1.append(stats.norm(centers[i], std).rvs(100))
plt.plot(np.arange(len(data_1[i]))+i*len(data_1[0]),data_1[i], '.', color = colors[i])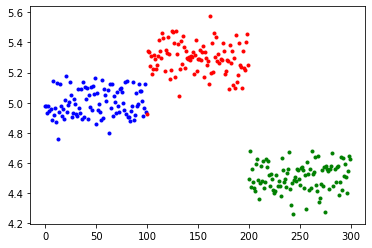
# 표준 편차를 2로 설정
std_2 = 2
data_2 = []
for i in range(3):
data_2.append(stats.norm(centers[i], std_2).rvs(100))
plt.plot(np.arange(len(data_1[i]))+i*len(data_2[0]), data_2[i], '.', color = colors[i])
이를 통해, 집단 평균값의 분산이 클수록 집단 내 분산이 작아질수록 평균의 차이가 분명해짐을 알 수 있다.
분산분석은 집단 간 분산과 집단 내 분산 두 가지를 이용한다.
일원 분산분석( One-way ANOVA )
종속 변인과 독립 변인의 집단이 1개인 경우이다.
한 가지 변수의 변화가 결과 변수에 어떤 영향을 미치는지 확인할 수 있다.
위의 페이지 예를 통해 ANOVA의 토대가 되는 재표본추출 과정을 살펴보면 다음과 같다.
1. 모든 데이터를 한 상자에 모은다.
2. 5개의 값을 갖는 4개의 재표본을 섞어서 추출한다.
3. 각 그룹의 평균을 기록한다.
4. 네 그룹 평균 사이의 분산을 기록한다.
5. 2 ~ 4 단계를 여러 번 반복한다.
다른 예로 살펴보자. ( Altman 910 )
22명의 심장 우회 수술을 받은 환자를 다음의 3가지 그룹으로 나누었다.
Group I: 50% 아산화 질소(nitrous oxide)와 50%의 산소(oxygen) 혼합물을 24시간 동안 흡입한 환자
Group II: 50% 아산화 질소와 50% 산소 혼합물을 수술 받는 동안만 흡입한 환자
Group III: 아산화 질소 없이 오직 35-50%의 산소만 24시간동안 처리한 환자
이후, 적혈구의 엽산 수치를 24시간 이후에 측정하였다.
# url로 데이터 얻어오기
url = 'https://raw.githubusercontent.com/thomas-haslwanter/statsintro_python/master/ipynb/Data/data_altman/altman_910.txt'
data = np.genfromtxt(urllib.request.urlopen(url), delimiter=',')data를 살펴보면 다음과 같다.
array([[243., 1.],
[251., 1.],
[275., 1.],
[291., 1.],
[347., 1.],
[354., 1.],
[380., 1.],
[392., 1.],
[206., 2.],
[210., 2.],
[226., 2.],
[249., 2.],
[255., 2.],
[273., 2.],
[285., 2.],
[295., 2.],
[309., 2.],
[241., 3.],
[258., 3.],
[270., 3.],
[293., 3.],
[328., 3.]])# 1번 열의 값에 따라 그룹 나눠주기
group1 = data[data[:,1]==1,0]
group2 = data[data[:,1]==2,0]
group3 = data[data[:,1]==3,0]
# 그려보기
plot_data = [group1, group2, group3]
ax = plt.boxplot(plot_data)
plt.show()
boxplot에서 볼 때, 평균값의 차이가 실제로 의미있는지 or 분산이 커서 차이가 있는지 애매하다.
이럴 때, 분산분석을 통해 통계적 유의성을 알아볼 수 있다.
stats.f_oneway(group1, group2, group3)f통계량을 바탕으로 하는 일원분산분석을 수행하면 다음과 같은 결과가 출력된다.
F_onewayResult(statistic=3.7113359882669763, pvalue=0.043589334959178244)일원분산분석 결과 F= 3.71134이다.
p-value는 0.05보다 작기 때문에 그룹의 평균값이 통계적으로 유의미하게 차이난다고 할 수 있다.
이원분산분석( two-way ANOVA )
독립변인의 수가 두 개 이상일 때 집단 간 차이가 유의한지 검증하는데 사용된다.
만약 페이지를 접속하는 수가 주말/평일에 따라 많은 영향을 받는다고 한다면, ( 페이지1주말, 페이지1평일, 페이지2주말, 페이지2주말 등 )의 데이터가 생성된다. 이 때 필요한 것이 이원ANOVA 이다. 이는 상호작용 효과를 확인하는 식으로 일원 ANOVA와 방식은 비슷하다.
총평균 효과와 처리 효과를 확인한 뒤, 각 그룹의 주말/평일 데이터를 따로 분리한다.
그리고 그 부분집합들에 대한 평균과 처리 평균 사이의 차이를 찾아본다.
다른 예로 살펴보자. ( altman_12_6 )
태아의 머리 둘레 측정 데이터이다. 4명의 관측자가 3명의 태아를 상대로 측정하였다. 이를 통해서 초음파로 태아의 머리 둘레 측정 데이터가 재현성이 있는지 조사하였다.
inFile = 'altman_12_6.txt'
url_base = 'https://raw.githubusercontent.com/thomas-haslwanter/statsintro_python/master/ipynb/Data/data_altman/'
url = url_base + inFile
data = np.genfromtxt(urllib.request.urlopen(url), delimiter=',')
data데이터를 살펴보면 다음과 같다.
0번 열은 측정 결과, 1번 열은 태아 번호, 2번 열은 관측자 번호이다.
array([[14.3, 1. , 1. ],
[14. , 1. , 1. ],
[14.8, 1. , 1. ],
[13.6, 1. , 2. ],
[13.6, 1. , 2. ],
[13.8, 1. , 2. ],
[13.9, 1. , 3. ],
[13.7, 1. , 3. ],
[13.8, 1. , 3. ],
[13.8, 1. , 4. ],
[14.7, 1. , 4. ],
[13.9, 1. , 4. ],
[19.7, 2. , 1. ],
[19.9, 2. , 1. ],
[19.8, 2. , 1. ],
[19.8, 2. , 2. ],
[19.3, 2. , 2. ],
[19.8, 2. , 2. ],
[19.5, 2. , 3. ],
[19.8, 2. , 3. ],
[19.5, 2. , 3. ],
[19.8, 2. , 4. ],
[19.6, 2. , 4. ],
[19.8, 2. , 4. ],
[13. , 3. , 1. ],
[12.6, 3. , 1. ],
[12.9, 3. , 1. ],
[12.4, 3. , 2. ],
[12.8, 3. , 2. ],
[12.5, 3. , 2. ],
[12.8, 3. , 3. ],
[12.7, 3. , 3. ],
[12.5, 3. , 3. ],
[13. , 3. , 4. ],
[12.9, 3. , 4. ],
[13.8, 3. , 4. ]])그려보자.
# column명 정의
df = pd.DataFrame(data, columns=['head_size', 'fetus', 'observer'])
# 태아별 머리 둘레 plot 만들기
df.boxplot(column = 'head_size', by='fetus' , grid = False)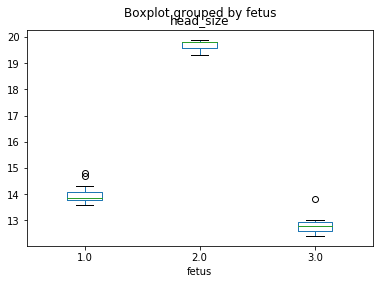
그림을 보니 태아 3명의 머리 둘레는 차이가 있는 듯 하다. 그렇다면 이것이 관측자와 상호작용이 있는지 분석해보자.
= 관측자가 누군지에 따라 머리 둘레에 영향이 있을까?
귀무가설 : 관측자와 태아의 머리둘레 값은 연관성이 없다.
대립가설 : 관측자와 태아의 머리둘레 값은 연관성이 있다.
formula = 'head_size ~ C(fetus) + C(observer) + C(fetus):C(observer)'
lm = ols(formula, df).fit()
print(anova_lm(lm))결과는 다음과 같다.
df sum_sq mean_sq F PR(>F)
C(fetus) 2.0 324.008889 162.004444 2113.101449 1.051039e-27
C(observer) 3.0 1.198611 0.399537 5.211353 6.497055e-03
C(fetus):C(observer) 6.0 0.562222 0.093704 1.222222 3.295509e-01
Residual 24.0 1.840000 0.076667 NaN NaNp-value가 0.05 이상이기 때문에 귀무가설을 기각할 수 없다.
즉, 측정자와 태아의 머리둘레값에는 연관성이 없다고 할 수 있다. 측정하는 사람이 달라도 머리 둘레 값은 일정하다는 것이다.
분산분석의 한계점
전체 그룹 간 평균값 차이가 통계적 의미가 있는지 판단하는데 유용하지만, 어느 그룹의 평균값이 의미가 있는지는 알기 어렵다. 따라서 추가적인 사후 분석이 필요하다.
통계적 공정관리
학교 수업에서 통계적 공정관리 과목을 들으며 직접 물건을 측정한 적이 있다. 조원 3명이서 10가지의 물품을 3번씩 번갈아가며 측정했다. 똑같은 물건이라도 몇번째에 하느냐에 따라, 누가 하느냐에 따라 측정 결과가 달랐다. 이제서야 실험의도를 깨달았다.......그것이 또 ANOVA로 가는 것이었는데....... 반성.......눈물........
'AI > Statistics' 카테고리의 다른 글
| 10. 멀티암드 밴딧 알고리즘( MAB;Multi-armed bandit ) (0) | 2020.05.20 |
|---|---|
| 09. 카이제곱 검정 ( chi-squared test ) (4) | 2020.05.18 |
| 07. 자유도( degree of freedom ) (6) | 2020.05.14 |
| 06. 다중 검정( Multiple Comparison ) (0) | 2020.05.13 |
| 05. t검정( t -test ) (0) | 2020.05.11 |
