카이제곱검정은 카이제곱 분포(chi-squared distribution)를 따른다.
카이제곱 분포란?
정규분포를 따르는 모집단에서 크기가 n인 표본을 무작위로 반복 추출한다. 이 때 각 표본의 분산들이 카이제곱 분포를 따른다고 한다. 자유도가 커질수록 정규분포에 가까워지며 다음과 같이 나타난다.

자유도가 k인 카이제곱분포의 확률밀도함수(pdf) 공식은 다음과 같다.

카이제곱 분포는 모분산에 대한 추정과 검정에 사용된다.
관측도수가 이론 상의 분포에 적합한지, 여러 집단 사이의 독립성 검정이 다른 특성에 영향을 미치는가에 대한 검정을 한다. 자료가 빈도로 주어졌을 때, 특히 명목척도 자료 분석에 이용된다.
카이제곱 검정방법
- 독립성 검정: 두 변수는 서로 연관성이 있는가 없는가?
- 적합성 검정: 실제 표본이 내가 생각하는 분포와 같은가 다른가?
- 동일성 검정: 두 집단의 분포가 동일한가? 다른 분포인가?
카이제곱 종류
1. 일원 카이제곱 검정 : 하나의 범주를 대상으로 한다 -> 적합성 검정
2. 이원 카이제곱 검정 : 두 개 이상의 범주를 대상으로 한다 -> 독립성, 동질성 검정
일원 카이제곱 검정( one-way chi-squared test )
제품의 판매량 비율은 다음과 같다.
A 56%, B 12%, C 32%
그런데, 특정 지역에 제품 A,B,C의 보유대수를 조사하니, 각각 324, 78, 261대 였다.
이를 토대로 관찰빈도와 기대빈도를 만들면 다음과 같다.
| 구분 | A | B | C | 계 |
| 관찰 빈도 | 324 | 78 | 261 | 663 |
| 기대 빈도 | 371 | 80 | 212 | 663 |
적합성검정
귀무가설 H0 : 관찰빈도 = 기대빈도
대립가설 H1 : 관찰빈도 ≠ 기대빈도
code
from pandas import DataFrame
# 관찰빈도
xo = [324, 78, 261]
# 기대빈도
xe = [371, 80, 212]
# df로
xc = DataFrame([xo, xe],
columns = ['A','B','C'],
index = ['Obs', 'Exp'])
xc
bar plot을 그려서 얼마나 차이가 나는지 보자 !
# bar plot을 그려보자
import matplotlib.pyplot as plt
%matplotlib inline
ax = xc.plot(kind='bar', figsize=(8,6))
ax.set_ylabel('value')
plt.grid(color='darkgray')
plt.show()
A, C의 차이가 큰 것으로 보인다.
카이제곱 통계량을 출력해보자.
from scipy.stats import chisquare
result = chisquare(xo, f_exp=xe)
resultPower_divergenceResult(statistic=17.329649595687332, pvalue=0.00017254977751013492)p-value가 0.0001725로 유의수준 0.05보다 아주 작으므로 귀무가설을 기각하고, 대립가설을 지지한다.
즉, 관찰빈도와 기대빈도는 다르다.
카이제곱 통계량을 plot으로 표시해보자.
1 ) 자유도 = 2일 때 카이제곱분포 그리기
2 ) 95%일 때, 기준이 되는 통계량 표시
3 ) 결과값이 어디에 위치하는지 표시
1 )
# 카이제곱분포의 플롯을 그려보자.
from numpy import linspace
from scipy.stats import chi2
df = 2 # 자유도
x = linspace(0, 20, 201)
y = chi2(df).pdf(x)
plt.plot(x,y,'b--')
plt.grid()
plt.show()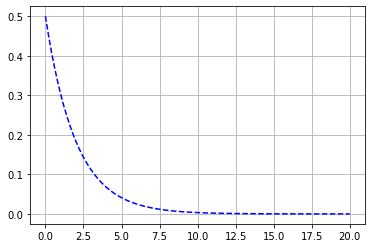
2 )
# 여기에서 수직선과 text를 이용하여 p-value의 위치를 표시해보자
x95 = chi2(df).ppf(.95)
plt.plot(x, y, 'b--')
plt.axvline(x=x95, color='lightcoral', linestyle=':')
plt.text(x95, .4, 'critical value = ' + str(round(x95, 4)),
horizontalalignment='center',color='lightcoral')
plt.grid()
plt.show()
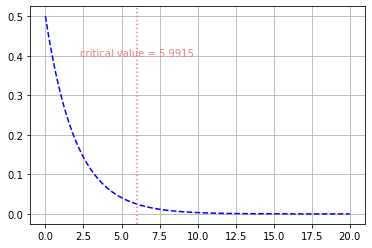
이 점선의 왼쪽은 귀무가설을 채택하는 영역이고, 오른쪽은 귀무가설을 기각하는 영역이다.
3 )
x95 = chi2(df).ppf(.95)
plt.plot(x, y, 'b--')
plt.axvline(x=x95, color='lightcoral', linestyle=':')
plt.text(x95, .4, 'critical value = ' + str(round(x95, 4)),
horizontalalignment='center',color='lightcoral')
# 위에서 구한 카이분포통계값 = result[0]
plt.axvline(x=result[0], color='purple', linestyle=':')
plt.text(result[0], .4, 'statistic '+ str(round(result[0], 4)),
horizontalalignment='center', color='purple')
plt.grid()
plt.show()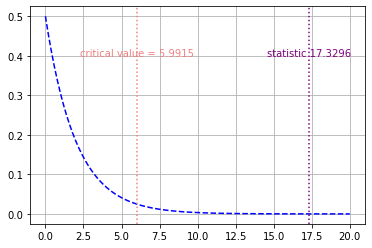
따라서 통계량은 critical value(임계치)의 오른쪽에 위치하므로 귀무가설을 기각한다.
이원 카이제곱 검정( two-way chi-squared test )
제품 1~3까지 여성, 남성의 판매량 차이에 대하여 카이제곱 검정을 해보자.
xf = [269, 83, 215]
xm = [155, 57, 181]
x = DataFrame([xf, xm],
columns = ['item1','item2','item3'],
index = ['Female','Male'])
x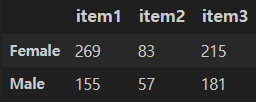
독립성 검정
귀무가설 : 성별과 아이템 품목 판매량은 관계가 없다.
대립가설 : 성별과 아이템 품목 판매량은 관계가 있다.
from scipy.stats import chi2_contingency
chi_2, p, dof, expected = chi2_contingency([xf, xm])
msg = 'Test Statistic: {}\np-value: {}\nDegree of Freedom: {}'
print(msg.format(chi_2, p, dof))
print(expected)
Test Statistic: 7.094264414804222
p-value: 0.028807134195296135
Degree of Freedom: 2
[[250.425 82.6875 233.8875]
[173.575 57.3125 162.1125]]p-value는 0.02881으로 유의수준 0.05보다 작은 값이므로 귀무가설을 기각한다.
따라서 성별과 아이템 품목 판매량은 관계가 있다.
-----
동질성 검정
귀무가설: 교육방법에 따른 교육생들의 만족도 차이가 없다.
대립가설: 교육방법에 따른 교육생들의 만족도 차이가 있다.
import pandas as pd
data = pd.read_csv("https://raw.githubusercontent.com/wjddyd66/R/master/Data/survey_method.csv")
print(data.head(5))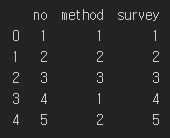
ctab = pd.crosstab(index=data["method"], columns=data["survey"])
print(ctab)
from scipy import stats
chi2, p, dof, expected = stats.chi2_contingency(ctab)
msg = "chi2:{}, p-value:{}, df:{}"
print(msg.format(chi2, p, dof))chi2:6.544667820529891, p-value:0.5864574374550608, df:8p-value(0.58) > 0.05(95% 신뢰확률에서의 유의수준) 이므로 귀무가설을 채택한다.
즉, 교육방법에 따른 교육생들의 만족도에 차이가 없다고 할 수 있다.
[R Studio] 카이제곱분포(chi-squared distribution) plot 그리기
R 과 R Studio에서 카이제곱분포(chi-squared distribution) plot 그리기정규분포를 따르는 모집단에서 ...
blog.naver.com
[파이썬 데이터 사이언스] 카이제곱 검정(chi-squared test)
01참고자료이 포스팅은 R을 활용한 통계 분석에 대하여 파이썬을 활용하여 재작성해보는 내용을...
blog.naver.com
DataAnalysis-카이제곱 검정
카이제곱 검정방법카이제곱 데스트는 그룹간에 차이가 있는지 여부(= 그룹끼지 독립이 아닌지의 여부)에 대해 Chisquare 분포를 사용해 가설검정을 하는 방법이다. 그룹간에 차이가 있는지 없는지
wjddyd66.github.io
'AI > Statistics' 카테고리의 다른 글
| 10. 멀티암드 밴딧 알고리즘( MAB;Multi-armed bandit ) (0) | 2020.05.20 |
|---|---|
| 08. 분산분석( ANOVA ) (0) | 2020.05.17 |
| 07. 자유도( degree of freedom ) (4) | 2020.05.14 |
| 06. 다중 검정( Multiple Comparison ) (0) | 2020.05.13 |
| 05. t검정( t -test ) (0) | 2020.05.11 |