나이브 베이즈 분류?
기본적으로 각 속성값 확률을 기반으로 범주에 속한 인스턴스를 확률로 결정한다. '나이브'는 다른 속성과 독립적이라는 의미로, 속성값은 다른 속성값과 관계가 없음을 의미한다.
베이즈 정리
매개변수 x,y가 있을 때, 분류1에 속할 확률이 p1(x,y) 이고, 분류 2 에 속할 확률이 p2(x,y)이면
* p1(x,y) > p2(x,y) 이면, 분류1
* p1(x,y) < p2(x,y) 이면, 분류2 이다.
다음의 예제로 공부해보자.

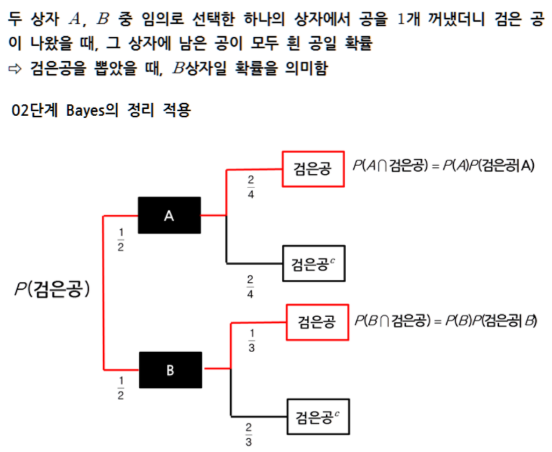

나이브 가정
나이브 베이즈 분류모형은 모든 차원의 개별 독립변수가 서로 조건부독립이라는 가정을 사용한다. '나이브'가 독립을 의미한다. 나이브 가정을 사용하면 벡터 x의 결합확률분포함수는 개별 스칼라 원소의 확률분포함수의 곱이 된다. 따라서 결합확률분포함수보다 추정하기 훨씬 쉽고, 가능도 함수를 추정한 후에는 베이즈 정리를 사용하여 조건부확률을 계산할 수 있다.
베르누이분포
각각의 x = ( x1, x2, ... , xn)의 각 원소 xd가 0 또는 1이라는 값만 알 수 있다.
전체 D * K의 동전이 존재하며 같은 클래스에 속하는 D개의 동전이 하나의 동전 세트를 구성하고 이러한 동전 세트가 K개 있다고 생각할 수 있다.

이러한 동전 세트마다 확률 특성이 다르므로 베르누이분포 가능도 모형을 기반으로 하는 나이브베이즈 모형은 동전 세트를 N번 던진 결과로부터 1, ... , K 중 어느 동전 시트를 던졌는지 찾아내는 모형이라고 할 수 있다.
CODE
전자우편과 같은 문서 내에 특정한 단어가 포함되어 있는지의 여부는 베르누이 확률변수로 모형화할 수 있다. 독립변수가 0 또는 1의 값을 가지면 베르누이 나이브베이즈 모형을 사용한다.
다음 데이터는 4개의 키워드를 사용하여 정상 메일 4개와 스팸 메일 6개를 BOW로 인코딩한 행렬이다. 예를 들어, 첫번째 메일은 정상 메일이고 1번 4번 키워드는 포함하지 않지만 2번 3번 키워드는 포함한다.
이 데이터를 베르누이 나이브베이즈 모형으로 예측해보자.
import numpy as np
from sklearn.naive_bayes import BernoulliNB
# X : 단어 포함시 1 미포함시 0
# y : 정상 메일 0 스팸 메일 1
X = np.array([
[0, 1, 1, 0],
[1, 1, 1, 1],
[1, 1, 1, 0],
[0, 1, 0, 0],
[0, 0, 0, 1],
[0, 1, 1, 0],
[0, 1, 1, 1],
[1, 0, 1, 0],
[1, 0, 1, 1],
[0, 1, 1, 0]])
y = np.array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1])model_bern = BernoulliNB().fit(X, y)
x_new = np.array([0, 1, 1, 1])
model_bern.predict_proba([x_new])array([[0.34501348, 0.65498652]])스팸일 확률이 더 높다
x_new = np.array([0, 0, 1, 1])
model_bern.predict_proba([x_new])array([[0.09530901, 0.90469099]])스팸일 확률이 더 높다
x_new = np.array([1, 1, 1, 0])
model_bern.predict_proba([x_new])array([[0.6371329, 0.3628671]])정상일 확률이 더 높다
다항분포
x = ( 1, 4, 0, 5 ) 라고 하자. 이는 4면체 주사위를 10번 던져서 1인 면이 1번, 2인 면이 4번, 3인 면이 0번, 4인 면이 5번 나온 결과로 해석된다. 각 클래스마다 주사위가 다르므로 K개의 클래스를 구분하는 문제에서 D개의 면을 가진 주사위가 k개 있다고 본다. 따라서 다항분포 가능도 모형 기반의 나이브베이즈 모형은 주사위를 던진 결과로부터 1, ... , K 중 어느 주사위를 던졌는지를 찾아내는 모형이라고 할 수 있다.
CODE
스팸 메일 필터링을 예로 들어보자. 위와 다른 점은 BOW 인코딩을 할 때, 각 키워드가 출현한 빈도를 직접 입력 변수로 사용한다.
X = np.array([
[3, 4, 1, 2],
[3, 5, 1, 1],
[3, 3, 0, 4],
[3, 4, 1, 2],
[1, 2, 1, 4],
[0, 0, 5, 3],
[1, 2, 4, 1],
[1, 1, 4, 2],
[0, 1, 2, 5],
[2, 1, 2, 3]])
y = np.array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1])from sklearn.naive_bayes import MultinomialNB
model_mult = MultinomialNB().fit(X, y)
x_new = np.array([10, 10, 10, 10])
model_mult.predict_proba([x_new])array([[0.38848858, 0.61151142]])스팸일 확률이 높다
x_new = np.array([4, 4, 2, 2])
model_mult.predict_proba([x_new])array([[0.96466932, 0.03533068]])정상일 확률이 높다
다항분포
CODE
from sklearn.naive_bayes import GaussianNB
X = np.array([
[0, 1, 1, 0],
[1, 1, 1, 1],
[1, 1, 1, 0],
[0, 1, 0, 0],
[0, 0, 0, 1],
[0, 1, 1, 0],
[0, 1, 1, 1],
[1, 0, 1, 0],
[1, 0, 1, 1],
[0, 1, 1, 0]])
y = np.array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1])
#X는 독립변수 데이터 셋, y는 종속변수 데이터 셋
model_NB = GaussianNB().fit(X, y)
x_new = np.array([0, 0, 0, 0])
model_NB.predict_proba([x_new])
array([[0., 1.]])
'AI > Experiment' 카테고리의 다른 글
| 08. 서포트 벡터 머신 ( support vector machine ) (0) | 2020.05.19 |
|---|---|
| 07. 로지스틱 회귀( Logistic Regression ) (0) | 2020.05.18 |
| 06. 선형 회귀의 한계점 (0) | 2020.05.17 |
| 05. 릿지 회귀, 라쏘 회귀 ( Ridge, Lasso ) (0) | 2020.05.15 |
| 04. 다항 회귀( Polynomial Regression ) (0) | 2020.05.14 |